Did you know that the angle of elevation and the angle of depression are always equal between two points? This is key in geometry and trigonometry, especially in applied math. It shows how important these angles are in fields like architecture, aviation, and surveying.
Understanding them is not just for theory. It’s crucial for solving real-world problems. By knowing these concepts, you can measure heights and distances accurately. This is vital in many jobs today. For deeper insights, check out angle of depression applications.
Key Takeaways
- The angle of elevation and the angle of depression are equal, forming alternate angles on parallel lines.
- Trigonometry is essential for solving problems involving heights and distances.
- Right-angled triangles can accurately represent the positions of objects at different heights.
- Converting angles into degrees, minutes, and seconds enhances precision in measurements.
- Understanding these angles can benefit various fields like architecture and aviation significantly.
Understanding Angles in Geometry
Angles are key to much of geometry. They help us figure out how different shapes relate. Each angle is made by two rays starting from the same point. You can measure them in degrees.
Angles have lots of uses in the real world. For example, to find out how tall something is, like the Seattle Space Needle. It’s about 604 feet tall. From its 220-foot shadow, we find a 70-degree angle to the top. This shows how angles help us in real life.
Understanding angles means seeing how they fit with flat surfaces. Think about a rock climber 631 feet up. If you stand 1,000 feet away and are 6 feet tall, you look up at a 32-degree angle. This helps us solve problems by understanding angles.
Knowing about angles helps in many areas, including building design and finding your way. Learning about angles makes tackling math challenges easier.
Definitions of Angle of Elevation and Depression
Understanding the angle of elevation and depression is key in geometry and trigonometry. These angles help relate distances and heights clearly. Knowing about them is crucial in many fields like architecture, surveying, and astronomy.
What is the Angle of Elevation?
The angle of elevation is where your line of sight meets something above you. Imagine looking up at a flagpole. If the angle up to the top is 50°, we can figure out the flagpole’s height from where we stand. This tells us the pole is about 23.8 feet tall. Making sure we measure this angle right is very important for building things safely.
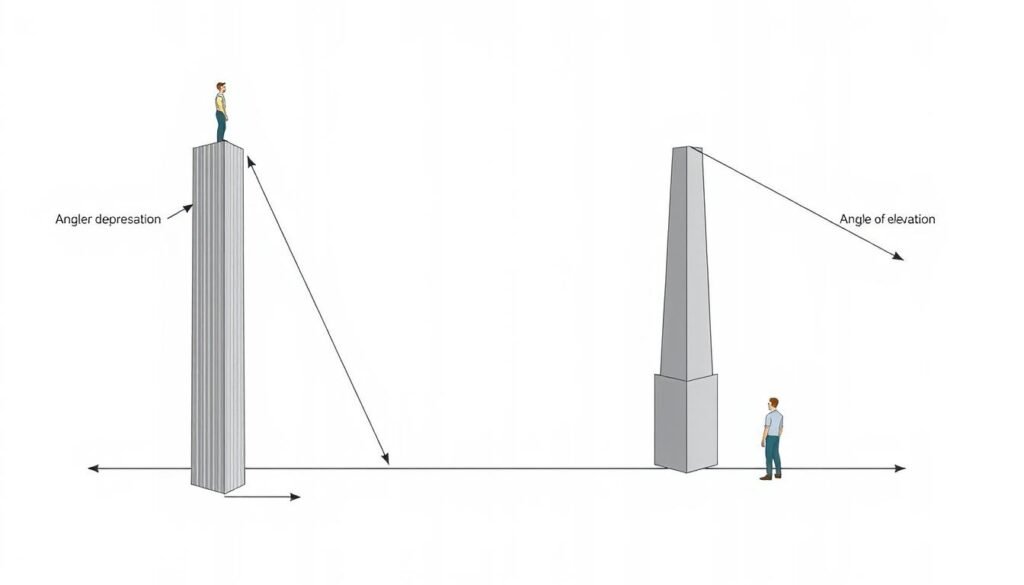
What is the Angle of Depression?
The angle of depression happens when you look down at something from above. Think of a pilot flying above a control tower. If the tower seems tilted by 10° downward from the plane, we can find the distance straight to it. This lets us know the tower is about 28,800 feet away. This measurement is super useful in aviation to figure out how high and far away things are.
Angle of Depression vs Angle of Elevation
Angle of depression and angle of elevation are key in geometry. They show a special kind of symmetry. The angle of elevation happens when you look up from a flat line to a higher point, like seeing a bird fly. The angle of depression is when you look down from a line to a lower point, like looking at a boat from a lighthouse.
These angles match up when lines are parallel. They form as alternate angles when a flat line meets two lines at different points. So, the angle you see from above matches the one from below, both from their own flat lines.
To figure out these angles, we use trigonometry. Sine is the height over the longest side, cosine is the side length over the longest side, and tangent is the height over the side length. This math helps in fields like engineering and architecture to make things safe and efficient.
| Type of Angle | Definition | Measurement Method | Application |
|---|---|---|---|
| Angle of Elevation | Angle formed when looking upwards from a horizontal plane | Calculated using the sine, cosine, and tangent ratios | Used in scenarios such as measuring heights of buildings or trees |
| Angle of Depression | Angle formed when looking downwards from a horizontal plane | Calculated similarly using trigonometric ratios | Common in fields like surveying and architecture for assessing depth or drop-offs |
Knowing about these angles helps in measuring heights and distances in real life. By learning angle of depression and elevation, one can apply this in many jobs.
Trigonometric Fundamentals
Trigonometry is key for solving problems with angles of elevation and depression. These angles fit well in right-angled triangles. This makes it easy to use trigonometric relationships to figure out unknown sizes. With sine, cosine, and tangent ratios, we can get precise measurements needed in the real world.
Using Trigonometry to Solve Problems
The angle of elevation helps find the heights of buildings or towers. It uses special trigonometric ratios. The formula looks like this:
- Tangent of the angle of elevation = Height of the Object / Distance from the object
This is written as Tan θ = Opposite Side/Adjacent Side. For example, say an observer sees an angle of elevation, θ, at 36 degrees. The height is 335 ft and the distance is 249 ft. With trigonometry, we can uncover different insights.
Right-Angled Triangles and Angles
The angle of depression is the flip side of the angle of elevation. It’s what you see when looking down from a straight line. These angles match when seen from different spots. When calculating a 150-ft distance to a tower with a 45-degree angle and the same height, it shows how trigonometry and right triangles work together.
Knowing these trigonometric basics is useful in many jobs, like in construction or navigation. For more on how angles are used, check out more about angles of elevation and depression.
Applications in Real-Life Scenarios
Angles of elevation and depression are key in different areas, such as architecture, aviation, and surveying. These angles help professionals make precise calculations. This can greatly affect their work.
Examples in Architecture and Design
Triangles play a big role in architecture to make buildings strong and stable. Stairs, roofs, and bridges use triangular shapes for support. Architects use trigonometry to figure out sizes and angles for safe, good-looking buildings.
Using the angle of elevation helps architects know how tall to make a structure. They base this on how far away it is from where they are standing. This ensures the designs work well.
Usage in Aviation and Surveying
Pilots and surveyors use angles of elevation and depression too. Pilots need them to take off and land safely. Surveyors use these angles to measure land and make accurate maps. Trigonometry helps them find distances, like how far a plane is from a radar.
| Field | Application | Trigonometric Function |
|---|---|---|
| Architecture | Height calculations for building designs | Sine, cosine |
| Aviation | Altitude adjustments during flight | Tangent, sine |
| Surveying | Land elevation and distance measurements | Tangent, cosine |
In the end, understanding angles of elevation and depression is essential in many fields. It shows how important trigonometry is in solving everyday problems.
Calculating Angles: Methods and Formulas
Understanding how to calculate angles is vital in trigonometry, especially with angles of elevation and depression. These calculations are key in many real-world situations. For example, they help measure the height of buildings or distances. They are also useful in navigation. Learning how to find elevation and depression angles can improve your problem-solving abilities.
Finding the Angle of Elevation
The angle of elevation is created between a horizontal line and the line of sight to an object above. To figure out this angle, we often use the tangent function. This is summarized by the formula:
tan(angle) = height / distance
This formula makes it simple to find the angle of elevation. Imagine an observer standing 155 meters from a mountain’s base and seeing its peak at a 66-degree angle. This shows the importance of the angle between the observer, the object, and their line of sight. Such formulas are necessary for calculating things like basketball hoop heights or the incline for a bike ramp.
Calculating the Angle of Depression
The angle of depression occurs when someone looks down from a horizontal line to an object below. Figuring out this angle involves a similar method to that of elevation angles. The tangent function is crucial here too:
tan(angle) = height / distance
With known measurements, you can find the angle of depression. Take a baseball fan 200 feet from home plate, seeing a 62-degree angle of depression from 176.6 feet up. This demonstrates how these calculations are applied. They are crucial in fields like architecture, aviation, and surveying for precise measurements.
| Scenario | Description | Calculation Method |
|---|---|---|
| Mountain Peak | 66 degrees with a distance of 155 meters | Elevation: Use tan(angle) = height/distance |
| Baseball Fan | 62 degrees from a height of 176.6 feet | Depression: Apply tan(angle) = height/distance |
| Bike Ramp | 20-degree angle with base length of 27.5 ft | Use elevation angle formulas for determination |
Regularly using these formulas helps us understand geometric challenges better. They show how angles connect to real-world scenarios. If you want to learn more, websites like Angle of Depression have extra examples and problems to practice with.
Using Angular Measurements in Practical Applications
Angular measurements are key in many areas like engineering, architecture, and surveying. Knowing about degrees, minutes, and seconds helps achieve the needed accuracy. This knowledge is vital for professionals working with complex angular measurements.
Measurement Units: Degrees, Minutes, and Seconds
Degrees, minutes, and seconds are used for angular measurements. They ensure accuracy in high-precision situations. Let’s look at what these units mean:
- Degrees: The main unit of measurement, with a full circle being 360 degrees.
- Minutes: Each degree is split into 60 minutes for better detail.
- Seconds: Each minute breaks down into 60 seconds for finest precision.
An angle like 12° 30′ 15″ stands for 12 degrees, 30 minutes, and 15 seconds. This precision matters in fields like surveying, where unit conversions greatly enhance measurement accuracy.
Conversions Between Different Units
Converting among these units is crucial for clear communication and angle assessment. In surveys, converting degrees to minutes and seconds is common:
| Degrees | Minutes | Seconds |
|---|---|---|
| 12 | 0 | 0 |
| 12.5 | 30 | 0 |
| 12.75 | 45 | 0 |
Understanding unit conversions helps experts switch between systems easily. Precision tools like theodolites require calculations that involve these conversions, as they can measure angles very accurately.
Examples to Illustrate Concepts
Understanding angles of elevation and depression is easier with illustrative examples. They are used in many practical scenarios. This makes trigonometric principles easier to grasp. Below, you’ll find two examples to show why they’re important.
Example 1: Angle of Elevation in Nature
Imagine a hiker looking at the top of a tree 30 meters away. If the angle to the tree’s top is 65°, the hiker needs to do some math. Using trigonometry, they figure out the tree’s height is around 25.3 meters. This shows how angle knowledge helps us understand nature.
Example 2: Angle of Depression from a Building
In a city, someone stands on a rooftop and looks down at the ground. The angle of depression is 33.69°, with the building standing 50 meters tall. They can find the distance to a point on the ground using math. This practical scenario helps explain angles of depression in cities.
For more details and illustrative examples on angles of elevation and depression, go to this resource. It’s full of insights on these concepts in the real world.
Additional Trigonometric Concepts
Understanding slopes and gradients is key to mastering more complex trigonometry. This knowledge is very useful in areas like engineering and architecture. It helps improve how we calculate angles of elevation and depression in different situations.
Understanding Slopes and Gradients
Slopes and gradients tell us how steep a line or surface is. In math, a slope is found by dividing the vertical change by the horizontal change. This is crucial for working out angles related to elevation and depression.
Consider the Space Needle’s 67-meter shadow and its 70° elevation angle. This gives us a height of about 184 meters. This example shows how these concepts are used in real-world situations.
Coordinate Geometry in Angles
Coordinate geometry helps us see how angles, distances, and slopes connect. It uses trigonometric ratios like tangent, sine, and cosine. These ratios find values we don’t know in real life.
Imagine a forest ranger spotting a fire from a 3° depression angle. They can calculate the fire is about 1717 feet away. This highlights how precise measurements lead to accurate results in real-life tasks.
Visualizing Angles in Geometry
Visual learning is key in understanding geometry. Angle visualization and diagrams help students grasp complex ideas. This approach makes abstract concepts more tangible.
Diagrams show relationships between angles of elevation and depression in a clear way. They make it easier to see how these angles work in real-life situations.
Graphs and Diagrams for Clarity
Graphs and diagrams are vital for visualizing geometry angles. They do not just show angles’ positions but also their real-world measurements. For example, the angle of elevation is the angle from the horizontal line to something above.
Meanwhile, the angle of depression goes downward from the horizontal to an object below. These diagrams help understand vertical and horizontal relationships. They make trigonometry principles easier to apply.
The Importance of Visual Learning
Visual learning helps students deeply understand math concepts. Seeing angles clearly in diagrams improves memory retention. Diagrams showing trigonometric functions let students visualize angles of elevation and depression.
This way, students see how these angles are used in architecture, surveying, and aviation. It aids in solving real-world problems and strengthens geometry knowledge.
| Application | Angle Type | Measurement Method |
|---|---|---|
| Surveying | Angle of Elevation | Theodolite |
| Architecture | Angle of Depression | Transit |
| Aviation | Angle of Elevation | GPS and Altitude Measurements |
| Engineering Design | Complementary Angles | Trigonometric Functions |
Common Mistakes to Avoid
When working on angles of elevation and depression, being careful about usual errors is key. These mistakes often come from wrong angle or calculation mishaps, changing how accurate your answers are. To get better at math, understand the small differences in viewing angles.
Misinterpreting Angles
A frequent mistake is mixing up angle types, like elevation and depression angles. This mix-up can cause wrong answers. Mistakes in angle views can happen if you don’t fully picture the situation or forget to mark your diagrams well. Knowing which angle you’re dealing with is crucial.
Errors in Calculations
When using sine, cosine, and tangent, calculation slips are common. These mistakes often stem from unclear problems or wrong unit use when changing angles to degrees or radians. Being precise at every step, and recalling basic principles, helps avoid such slips. Check out this guide on trigonometric concepts for more help.
| Error Type | Description | Prevention Tips |
|---|---|---|
| Angle Misinterpretation | Confusing angle of elevation with angle of depression | Carefully label diagrams and references |
| Calculation Errors | Incorrect application of trigonometric functions | Double-check each calculation step |
| Unit Conversion Mistakes | Errors in switching between degrees and radians | Use a calculator and verify conversions |
| Diagrams without Reference | Missing context leads to incorrect angle assumptions | Always review the context of the diagrams |
Practice Problems and Exercises
To really understand angles, it helps to work with practice problems. We’ve got a variety of problems here that will test your knowledge of angles of elevation and depression. Working through these problems will help you get better at geometry.
Each problem has a detailed solution. This way, you learn by doing, which is a great way to understand geometry deeply.
Sample Problems for Mastery
- Julia observes a car from a cliff. The angle of depression is 47°. If the cliff is 30 meters high, how far is the car from the base of the cliff?
- Philip looks down from a lighthouse at a ship below. The angle of depression is 23°40′ from a height of 42 meters. Calculate the horizontal distance from the base of the lighthouse to the ship.
- A bulldozer climbs a hill with an angle of elevation of 38°10′. If the bulldozer travels horizontally 120 meters, how high does it rise?
- Joy is sitting in a treetop 3.5 meters above the ground, observing Fritz the cat 2 meters away horizontally. What is the angle of elevation from Joy to Fritz?
- From a distance of 20 meters, the angle of elevation to the top of a flagpole is 32°. What is the height of the flagpole?
Tips for Solving Angles in Geometry
- Draw diagrams for visual clarity; it helps to conceptualize problems involving angles.
- Apply trigonometric functions like sine, cosine, and tangent to relate angles with side lengths.
- Always convert angles to the same unit when performing calculations.
- Practice regularly through various exercises for a better grasp of different angle scenarios.
Using these practice problems can really boost your skills and confidence in geometry. By working on these exercises regularly, you’ll get better at solving angle problems. This will help you master geometry.
| Problem | Angle | Height/Distance | Solution |
|---|---|---|---|
| 1 | 47° | 30 meters | Car distance: approx. 39.9 meters |
| 2 | 23°40′ | 42 meters | Distance to ship: approx. 181.5 meters |
| 3 | 38°10′ | 120 meters | Height rise: approx. 68.8 meters |
| 4 | Calculate | 3.5 meters (height of Joy) | Angle to Fritz: approx. 30.1° |
| 5 | 32° | 20 meters | Height of flagpole: approx. 12.6 meters |
Conclusion
In this summary, we looked at angles of depression and elevation. They are key in trigonometry and have many real-world uses. These concepts help measure heights and distances in many professions like architecture and aviation.
The article stressed the value of these mathematical ideas. They are crucial for using trigonometry in real life. Using ratios like tangent, sine, and cosine, people solve practical problems. This includes figuring out heights and distances.
Understanding these angles helps not just in school but in solving daily challenges. They are vital tools in math that help visualize and apply trigonometry in many ways.